《幂函数》导学案
姓名: 小组: 评价: .
课程标准
1、通过具体实例了解幂函数的实际意义，理解幂函数的概念。
2. 能够画出具体幂函数的图象，探索并理解幂函数的单调性与特殊点。
学习目标
1．通过具体实例，能够说出幂函数的概念，并能判断所给函数是否为幂函数；
2．通过画出具体幂函数的图象研究并提炼出幂函数的性质；
3. 通过实例能够对幂函数的图象和性质进行简单应用。
重点难点
1.从几个（五个+三个）具体幂函数中认识幂函数的一些性质.
2.画几个（五个+三个）幂函数的图象并由图象概括其性质
学科方法 数形结合 由特殊到一般
学科素养 数学抽象 逻辑推理 直观想象
学习任务一
1、幂函数的定义
一般地，形如
的函数称为幂函数（power functin），其中
是自变量，
是常数.
自我检测1：判断在函数
中，哪几个函数是幂函数？
自我检测2：已知幂函数过点（2，
），试求其解析式？
2、
幂函数的图象与性质
五个常用函数
思考：研究幂函数的图象与性质是在不同坐标系下还是同一坐标系下？
研究幂函数的哪些性质？
如何对
进行分类？
先做出： 的图象，归纳 的图象与性质
再作出： 的图象，归纳 的图象与性质
再作出： 的图象，归纳 的图象与性质
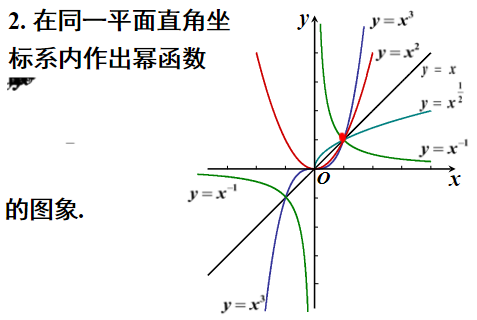
请按小组在同一坐标系下中作出下列幂函数的图象，并思考作图方法可以利用函数的什么性质进行优化？你发现了它们有什么共同的变化规律？
从函数的定义域、值域、单调性、奇偶性、公共点等方面归纳出本组函数特征
一小组
请归纳本组特征：
二小组
请归纳本组特征：
三小组
请归纳本组特征：
 |
|
|
|
0 |
1 |
4 |
9 |
 |
|
|
|
|
|
|
|
 |
-27 |
-8 |
-1 |
0 |
1 |
8 |
27 |
 |
|
|
|
|
|
|
|
观察图象，结合课本归纳概括幂函数的性质及图象变化规律，并完成以下填空（注意是共有的性质与规律）：
（Ⅰ）所有的幂函数在 都有定义，并且图象都过点 ；
（Ⅱ）当
时，图像过 点，并且在区间 上是 函数．
当
时，图像呈现 趋势；
越大图象向上越
.
当
时，图像呈现 趋势；
越小图象向上越
.
（Ⅲ）当
时， 图象与坐标轴 ，并且在区间 上是 函数．在第一象限内，当x从右边趋向原点时，图象在y轴右方无限地逼近y轴正半轴，当
趋于
时，图象在
轴上方无限地逼近
轴正半轴．
（Ⅳ）几个幂函数图象在直线
的右侧，自下而上（逆时针旋转）
依次
.
（Ⅴ）当
为 时，图象关于 对称，幂函数是奇函数；
当
为 时，图象关于 对称，幂函数是偶函数；
学习任务二 首先独立思考探究，然后合作交流展示
例1 函数
是幂函数，且在
上是减函数，则实数
m的取值集合是( )
A．{
m|
m＝－1或
m＝2} B．{
m|－1<
m<2} C．{2} D．{－1}
变式训练 幂函数
的图象与两坐标轴都无公共点，且关于y轴对称，求m的值
学习任务三 探究学习，迁移应用
例2 图中曲线是幂函数
在第一象限的图像．已知
n取
四个值，则相应于曲线
的
n依次为( )
A．
B．
C．
D．
变式训练 函数
的图象大致是 （ ）
例3 据幂函数的相关性质求解
已知不等式
成立，求
的取值范围？
变式：
小结提升
1、今天学习哪一类基本函数？它们的定义是怎么描述的？
2、你能根据5个函数图象说出有关幂函数的性质吗？
3、试归纳从哪些方面研究这三类基本初等函数？
当堂检测
1. 设
α∈{－2，－1，－
2，
2，1,2,3}，则使
f(
x)＝
xα为奇函数，且在(0，＋∞)上递增的
α的值的个数是( )
A．1 B．2 C．3 D．4
2. 若幂函数
y＝
f(
x)的图像经过点(2，)，则
f(25)的值是________．
3.比较两个数的大小:
4.幂函数
，
的图象中，
（1）关于原点对称，且通过原点，则
为 .
（2）不过原点，且不与坐标轴相交，则
为 .
（3）关于y轴对称，并与坐标轴相交，则
为 .
（4）图象是上凸慢增的，则
为 .
能力提高：设
适合不等式
，若
，
，当
时，则
A.
B.
C.
D.
课后挑战：已知函数
，试比较
与
的大小.
布置作业 按照本班老师要求完成对应作业
初中数学
